<< article précédente : l’origine des thermiques
Pour cette 2eme partie consacrée à l’étude des thermiques, dans la continuité du processus du développement des thermiques, on se focalisera sur des notions en lien avec l’échauffement des sols. L’élévation de la température des sols étant indispensable pour l’échange de chaleur avec la masse d’air en contact.
La température diffusée dans le sol est une fonction croissante de l’agitation moléculaire. Dans notre solide, ici le sol, l’agitation moléculaire élevée de la zone chaude communique de l’énergie aux zones les plus froides par le phénomène appelé conduction de chaleur. De plus, la propagation de la chaleur s’effectue également par les électrons libres.
La conduction est un phénomène de diffusion qui permet donc à la chaleur de se propager à l’intérieur d’un corps solide.
L’intensité de la conduction thermique dans le sol sera en fonction de la densité du milieu, de la mobilité des molécules et des gradients thermiques.
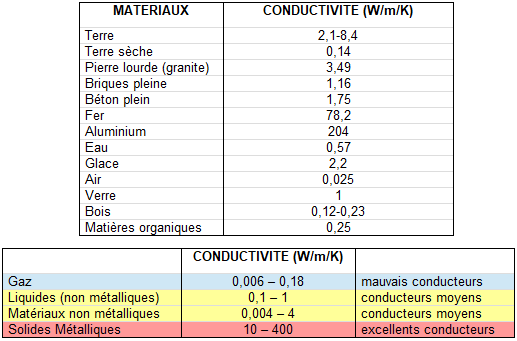
Le tableau ci dessous donne les valeurs de conductivité pour différents types sols :
On peut donc estimer pour 2 natures de sol différentes, toutes les 2 dans un environnement identique et propice aux déclenchements de thermiques, que les cycles thermiques d’un sol labouré (8.4W/m/K) aura une fréquence plus élevée que la roche (3.49W/m/K). Cela résulte de la différence de conductivité, soit une vitesse plus élevée de transmission de la chaleur pour le sol labouré.
Comme vu en première partie, lorsque le flux de chaleur issu du rayonnement solaire non réfléchi (Cf. albédo: première partie) parvient au sol, la variation du flux dépendra de l’orientation du sol par rapport au rayonnement solaire. Et dans l’idéal, le flux de chaleur optimal serait obtenu avec un rayonnement solaire perpendiculaire au sol.
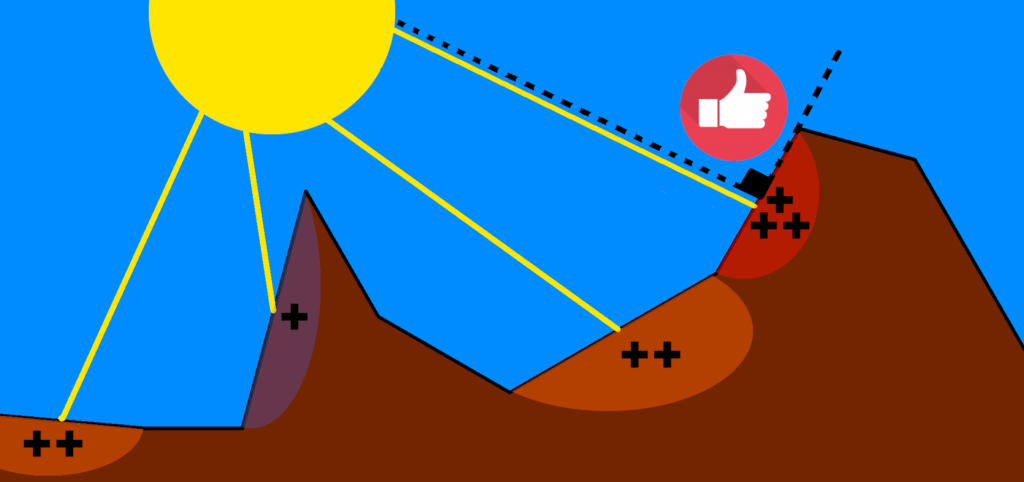
Le gradient de température (gradT) en chaque point représenté ci-dessous, est perpendiculaire à l’isotherme passant par ce point.
Par définition, le gradient de température correspond à la variation de température entre 2 points, soit entre 2 surfaces isothermes T1 et T2 par exemple :
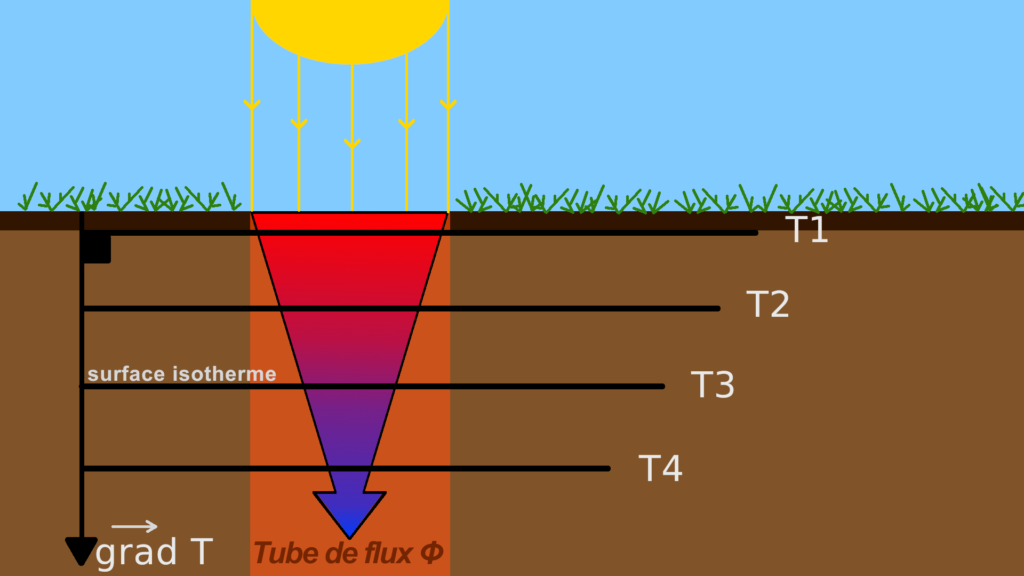 T1, T2, T3, T4 : température des surfaces isothermes
T1, T2, T3, T4 : température des surfaces isothermes
gradT : gradient de température
Et dans le sol, la densité de flux Φ est proportionnelle au gradient de température selon Fourrier :
 λ: conductivité du sol, constante positive caractéristiques du matériau (W/m/K).
λ: conductivité du sol, constante positive caractéristiques du matériau (W/m/K).
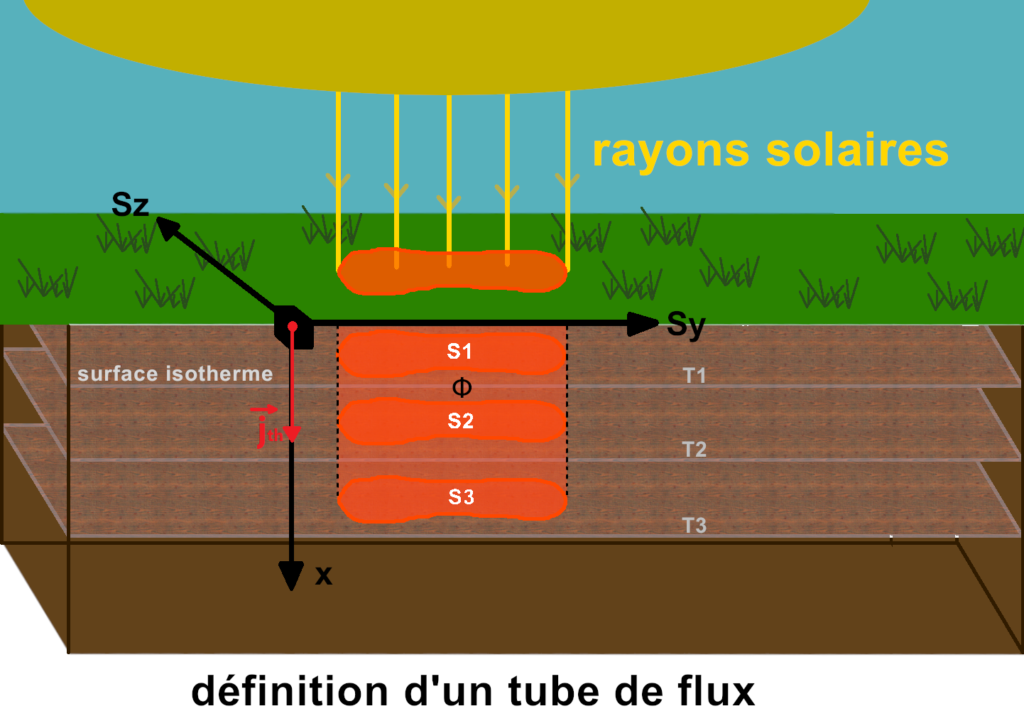
Les lignes de flux étant des surfaces adiabatiques, soit l’impossibilité à un flux de les traverser, les surfaces représentées ci-dessous (S1,S2,S3) sont donc traversées par le même flux. On obtient un tube de flux laissant passer le flux Φ :
Pour mieux appréhender la notion de conductivité, nous pouvons définir la notion de résistance thermique RthΦ, semblable à la loi d’Ohm en électricité :
 T1, T2 : température des surfaces isothermes
T1, T2 : température des surfaces isothermes
En référence à l’image ci-dessus, on considère la quantité d’énergie notée dQ, traversant par conduction thermique une surface S perpendiculaire à l’axe x perdant une durée notée dt dans le sens de l’axe x :
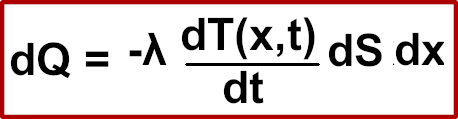 dT(x,t) : variation de température fonction de la profondeur x et du temps t
dT(x,t) : variation de température fonction de la profondeur x et du temps t
jth : vecteur du flux thermique
dS : variation de la surface
dx : variation sur l’axe x
Dans cette formule, on met également en évidence la conductivité notée λ.
Ainsi, la quantité d’énergie dQ reçue par de sol est une fonction croissante de la conductivité λ.
Cette quantité d’énergie varie dans le temps et peut s’exprimer de la façon suivante :
 dQ/dt : variation de la quantité d’énergie reçue dans le temps
dQ/dt : variation de la quantité d’énergie reçue dans le temps
jth : vecteur du flux thermique
dS : variation de la surface
Pour récapituler, le transfert thermique s’effectue :
- des zones plus chaudes vers les zones plus froides,
- proportionnellement à la surface à travers laquelle on évalue la puissance diffusée ainsi qu’à la durée du transfert,
- par augmentation de manière linéaire avec le gradient de température,
- en fonction de la densité, de la teneur en eau, de la minéralogie et de la taille de l’agencement des grains.
Abordons la question suivante :
quel est l’impact de l’humidité dans le sol sur le transfert de chaleur après une période pluvieuse par exemple ?
Les constituants du terrain ont une importance sur la sensibilité du bilan énergétique au sol, fonction de la capacité calorifique et de la conductivité.
Nous rencontrons principalement 3 constituants dans notre sol :
- le(s) solide(s)
- l’eau
- l’air
Et pour exemple, voici un aperçu de la conductivité thermique λ en fonction du contenu volumique en eau à 10°C et de la nature du sol :
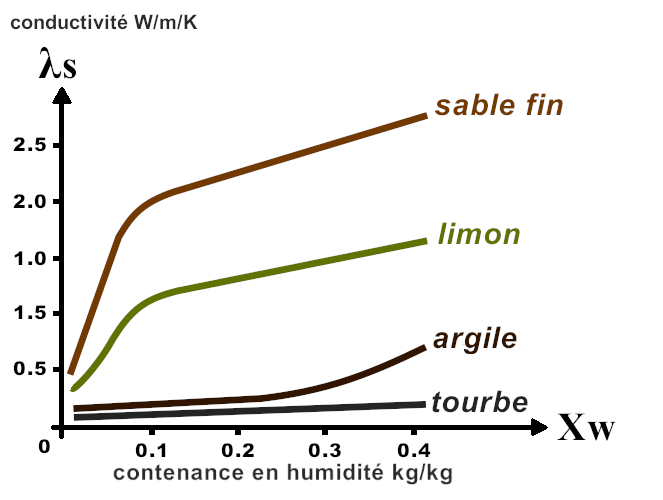 Il en résulte que la conductivité est fonction croissante de la teneur en eau mais différente selon la nature du sol. Un sol saturé en eau se réchauffera et se refroidira plus vite qu’un sol non saturé en eau.
Il en résulte que la conductivité est fonction croissante de la teneur en eau mais différente selon la nature du sol. Un sol saturé en eau se réchauffera et se refroidira plus vite qu’un sol non saturé en eau.
En plus de son influence sur la conductivité, l’eau contenu dans le sol joue également un rôle sur la capacité thermique. Abordons dès à présent la notion de la capacité calorifique.
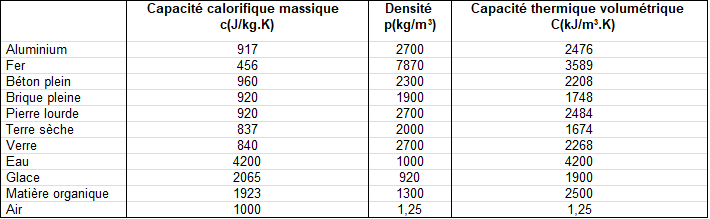
La capacité calorique, connu également sous le nom de capacité thermique volumique du sol C(J/m3.K), est l’énergie requise pour augmenter la température d’un volume unitaire de 1K (K=°C+273,5).
Son expression est donnée par le produit de la capacité calorifique massique c(J/kg.K) et de la masse volumique p(kg/m^3).
La capacité thermique volumétrique C(J/m^3.K) du sol caractérise l’aptitude du sol à emmagasiner l’énergie par la formule :
On peut donc envisager que :
plus la capacité thermique du sol est importante, plus la chaleur échangée avec l’air sera importante, plus l’écart de température entre l’air chauffé et l’air environnant sera élevé et plus la vitesse verticale des thermiques croira.
Biensûr, cette cause à effet doit prendre en considération le profil de température de l’air, l’humidité, les différents types de sols à proximité etc.
Et Selon De Vries (1963), la capacité calorifique du sol prenant en compte les solides et l’eau :
 Cth : capacité thermique volumétrique totale
Cth : capacité thermique volumétrique totale
Cthm : capacité thermique volumétrique des matières minérales présentes dans le sol
Ctho : capacité thermique volumétrique des matières organiques présentes dans le sol
Cthl : capacité thermique volumétrique des liquides présents dans le sol
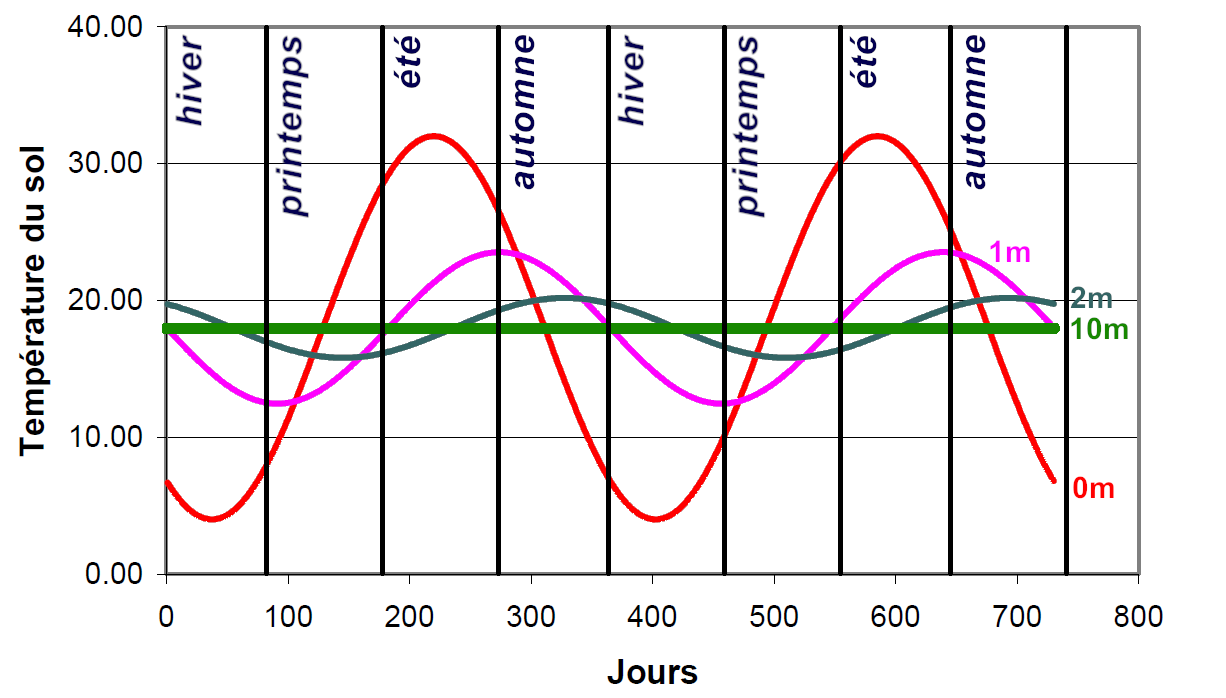
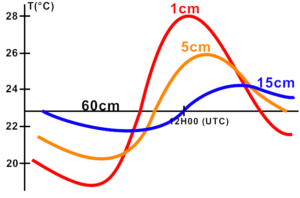
Il est important de remarquer que la conductivité et la capacité thermique du sol ont une influence considérable sur la variation de température en fonction de la profondeur dans le sol et du temps :
On en déduit que l’énergie radiatif de la première couche du sol fournit à l’atmosphère, par phénomène conducto-convectif, est celle ayant un importance significative dans la vie des thermiques. En effet, Après une pluie intense suivi d’un ensoleillement, la couche de surface se dessèchera plus rapidement que les couches plus profonde gardant leur humidité.
En lien avec la conductivité et la capacité thermique, la diffusivité intervient également dans les cycles thermiques. Elle exprime le rayon d’influence et la vitesse de transfert de la température dans le sol. Ainsi, plus la diffusivité thermique est importante, plus le sol est capable d’échanger rapidement et considérablement la température.
On peut donc envisager que :
plus le sol a les propriétés à se chauffer rapidement, plus les cycles seront rapprochés l’un de l’autre. Biensûr, il s’agit d’un maillon parmi d’autres dans la production des thermiques.
La diffusivité ⍺ est exprimée en mm²/s et est le rapport entre la conductivité thermique λ et la capacité thermique volumétrique C, soit :
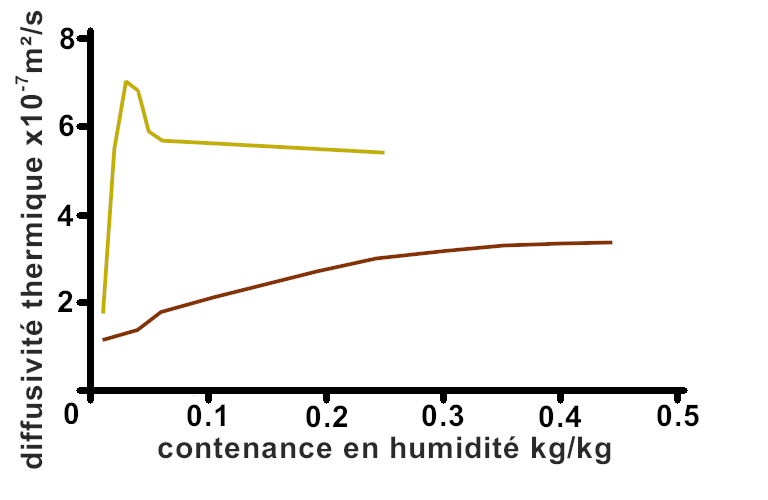
Compte tenu de ces éléments constituant nos sol (solide, air, eau), une expérience mené par Abu-Hamdeh (2003) corréla les résultats obtenus avec ceux des calculs effectués sur les effets de la densité et de la teneur en eau sur 2 types de sol. Il a donc comparé l’argile et le sable avec une teneur différente en eau :
L’échauffement des sols est un phénomène compliqué mais un passage nécessaire à la formation des thermiques que nous, “volatiles” parmi d’autres, exploitons pour le plaisir de voler plus longtemps et plus loin. Cette approche vous sera utile pour l’article qui suivra.
Au prochain article, nous nous concentrerons sur l’échange de chaleur entre le sol et l’air. Une différence de température entre l’air environnant et celui chauffé par le sol en résultera. Et par la poussée d’Archimède, nous serons en présence d’une masse d’air “chaude” ascendante ! Phénomène semblable aux montgolfières.


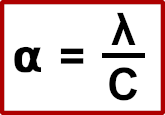
Répondre